Cách Tìm Số Nghiệm Của Phương Trình Bằng Máy Tính

by

Cách Tìm Số Nghiệm Của Phương Trình Bằng Máy Tính

Trong bài viết này Diễn đàn Toán Casio sẽ trình diễn cách sử dụng máy tính Casio fx 580 vnx để tìm và kiểm tra số nghiệm của một phương trình lượng giác. Bên cạnh đó, bài viết còn đưa ra thêm 1 số ít chiêu thức biện luận khác để xử lý bài toán trên .
Đang xem : Cách tìm số nghiệm của phương trình bằng máy tính

Bài toán tìm số nghiệm của phương trình lượng giác thường gây ra nhiều trở ngại cho các bạn học sinh. Do đó, trong bài viết này Diễn đàn Toán Casio sẽ trình bày cách sử dụng máy tính Casio fx 580vnx để tìm và kiểm tra số nghiệm của một phương trình lượng giác. Bên cạnh đó, bài viết còn đưa ra thêm một số phương pháp biện luận khác để giải quyết bài toán trên.

Phương pháp sử dụng Casio fx 580VNX để tìm số nghiệm của phương trình lượng giác:

Đưa phương trình về dạng $fleft( x
ight)=0$Dùng phương thức TABLE lập bảng giá trị của $fleft( x
ight)$ trên khoảng $left( a;b
ight)$Số lần đổi dấu của $fleft( x
ight)$ là số nghiệm của phương trình trên khoảng $left( a;b
ight)$

Bài toán 1. Xác định số nghiệm của phương trình $cos x=dfrac{13}{14}$ trên đoạn $left< -dfrac{pi }{2};2pi ight>$

A. 2 B. 3 C. 4 D. 5

Hướng dẫn giải

Cách 1. Giải bằng Máy tính Casio fx 580VNX

Chuyển máy tính về chính sách Radian qw22
Cài đặt đo lường và thống kê TABLE với một hàm số qwRR11
Vào phương pháp TABLE w8

Nhập vào hàm số $fleft( x
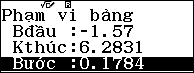
ight)=cos x-dfrac{13}{14}$ và bảng giá trị $Start=-dfrac{pi }{2}$, $End=2pi $, $Step=dfrac{2pi +dfrac{pi }{2}}{44}$

*
*

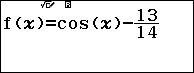
Nhắc lại: Giá trị hàm số $fleft( x
ight)$ đổi dấu khi đi qua $x={{x}_{1}}$ và $x={{x}_{2}}$ thì phương trình $fleft( x
ight)=0$ sẽ có một nghiệm trong khoảng $left( {{x}_{1}};{{x}_{2}}
ight)$

Quan sát bảng hiệu quả, ta nhận thấy

Ở hàng thứ 7 và hàng thứ 8, $fleft( x
ight)$ đổi dấu.

Suy ra phương trình $fleft( x
ight)=0$ có một nghiệm thuộc $left( -0.499;-0.321
ight)$

*

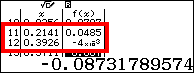
Ở hàng thứ 11 và hàng thứ 12, $fleft( x
ight)$ đổi dấu.

Xem thêm : Giải Vở Bài Tập Ngữ Văn 9 Tập 1 Ngắn Nhất, Soạn Bài Cụm Danh Từ Năm 2021 Mới, Ngắn Nhất

Suy ra phương trình $fleft( x
ight)=0$ có một nghiệm thuộc $left( 0.2141;0.3926
ight)$

*

Ở hàng thứ 42 và hàng thứ 43, $fleft( x
ight)$ đổi dấu.

Suy ra phương trình $fleft( x
ight)=0$ có một nghiệm thuộc $left( 5.7476;5.9261
ight)$

*

Vậy phương trình đã cho có 3 nghiệm trên đoạn USD left < - dfrac { pi } { 2 } ; 2 pi ight > USD
Đáp án B

Cách 2. Dùng đường tròn lượng giác

Biểu diễn cung từ USD – dfrac { pi } { 2 } USD đến USD 2 pi USD trên một đường tròn lượng giác và kẻ đường thẳng USD x = dfrac { 13 } { 14 } USD

*

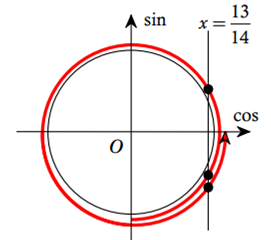
Quan sát hình vẽ ta thấy đường thẳng USD x = dfrac { 13 } { 14 } USD giao với cung lượng giác tại 3 điểm
Vậy phương trình đã cho có 3 nghiệm trên đoạn USD left < - dfrac { pi } { 2 } ; 2 pi ight > USD
Đáp án B

Cách 3.

Xem thêm : Cách Cắt Video Trên Youtube Bằng Máy Tính Windows 10 ( Mới Nhất 2021 )

Phương pháp tự luận

$cos x=dfrac{13}{14}Leftrightarrow x=pm arccos dfrac{13}{14}+k2pi left( kin mathbb{Z}
ight)$

TH1. USD x = arccos dfrac { 13 } { 14 } + k2pi USD
Ta có USD xin left < - dfrac { pi } { 2 } ; 2 pi ight > USD, nên USD – dfrac { pi } { 2 } le arccos dfrac { 13 } { 14 } + k2pi le 2 pi USD USD o – 0.3105 le kle 0.9394 USD
Suy ra USD k = 0 USD. Khi đó USD x = arccos dfrac { 13 } { 14 } USD

*

Ta có USD xin left < - dfrac { pi } { 2 } ; 2 pi ight > USD, suy ra USD – dfrac { pi } { 2 } le – arccos dfrac { 13 } { 14 } + k2pi le 2 pi USD USD o – 0.1894 le kle 1.0605 USD
TH2. USD x = – arccos dfrac { 13 } { 14 } + k2pi USD
Suy ra USD k = 0, k = 1 USD. Khi đó USD x = – arccos dfrac { 13 } { 14 }, x = – arccos dfrac { 13 } { 14 } + 2 pi USD

*

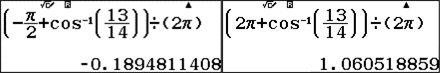
Đáp án B

Vậy phương trình đã cho có 3 nghiệm trên đoạn $left< -dfrac{pi }{2};2pi ight>$

Để có thêm nhiều ví dụ về dạng toán tìm số nghiệm của phương trình lượng giác, mời bạn đọc đón đọc những phần tiếp theo của chủ đề này .

Mọi ý kiến đóng góp và các câu hỏi thắc mắc về các bài viết hướng dẫn giải toán casio cũng như các vấn đề về máy tính Casio fx 580vnx, bạn đọc có thể gởi tin nhắn trực tiếp về fanpage DIỄN ĐÀN TOÁN CASIO

Xem thêm bài viết thuộc chuyên mục: Cách tính

Điều hướng bài viết