Bạn đang đọc: ✅ Cách giải nhanh bất phương trình bậc 2 ⭐️⭐️⭐️⭐️⭐
2/5 – ( 1 bầu chọn )
Bất phương trình quy về bậc hai
Tam thức bậc hai
– Tam thức bậc hai so với x là biểu thức có dạng f ( x ) = ax2 + bx + c, trong đó a, b, c là những thông số, a ≠ 0 .
* Ví dụ: Hãy cho biết đâu là tam thức bậc hai.
a ) f ( x ) = x2 – 3 x + 2
b ) f ( x ) = x2 – 4
c ) f ( x ) = x2 ( x-2 )
° Đáp án: a) và b) là tam thức bậc 2.
1. Dấu của tam thức bậc hai

Nhận xét:
![]()
* Định lý: Cho f(x) = ax2 + bx + c, Δ = b2 – 4ac.
– Nếu Δ < 0 thì f ( x ) luôn cùng dấu với thông số a với mọi x ∈ R . – Nếu Δ = 0 thì f ( x ) luôn cùng dấu với thông số a trừ khi x = - b / 2 a .
– Nếu Δ>0 thì f(x) luôn cùng dấu với hệ số a khi x < x1 hoặc x > x2 ; trái dấu với hệ số a khi x1 < x < x2 trong đó x1,x2 (với x1 – Tìm nghiệm của tam thức – Bất phương trình bậc 2 ẩn x là bất phương trình có dạng ax2 + bx + c < 0 ( hoặc ax2 + bx + c ≤ 0 ; ax2 + bx + c > 0 ; ax2 + bx + c ≥ 0 ), trong đó a, b, c là những số thực đã cho, a ≠ 0 . * Ví dụ: x2 – 2 >0; 2×2 +3x – 5 <0; – Giải bất phương trình bậc hai ax2 + bx + c < 0 thực ra là tìm những khoảng chừng mà trong đó f ( x ) = ax2 + bx + c cùng dấu với thông số a ( trường hợp a < 0 ) hoặc trái dấu với thông số a ( trường hợp a > 0 ) . Ví dụ: Giải bất phương trình Mẫu thức là tam thức bậc hai có hai nghiệm là 2 và 3 Để giải phương trình, bất phương trình chứa ẩn trong dấu GTTĐ, ta thường sử dụng định nghĩa hoặc đặc thù của GTTĐ để khử dấu GTTĐ . Trong các dạng toán thì bất phương trình chứa căn được xem là dạng toán khó nhất. Để giải phương trình, bất phương trình chứa ẩn trong dấu căn ta cầ sử dụng kết hợp các công thức giải bất phương trình lớp 10 kết hợp với phép nâng luỹ thừa hoặc đặt ẩn phụ để khử dấu căn. Muốn giải hệ bất phương trình bậc nhất một ẩn ta giải từng bất phương trình của hệ rồi lấy giao những tập nghiệm thu sát hoạch được . ∙ Dạng : P ( x ). Q ( x ) > 0 ( 1 ) ( trong đó P ( x ), Q. ( x ) là những nhị thức bậc nhất. ) ∙ Tương tự như giải pt chứa ẩn trong dấu GTTĐ, ta hay sử dụng định nghĩa và đặc thù của GTTĐ để khử dấu GTTĐ . * Ví dụ 1 (Bài 1 trang 105 SGK Đại Số 10): Xét dấu các tam thức bậc hai: a ) 5×2 – 3 x + 1 Lời giải ví dụ 1 (Bài 1 trang 105 SGK Đại Số 10): a ) 5×2 – 3 x + 1 * Ví dụ 2 (Bài 2 trang 105 SGK Đại Số 10): Lập bảng xét dấu của biểu thức a ) f ( x ) = ( 3×2 – 10 x + 3 ) ( 4 x – 5 ) ° Lời giải ví dụ 2 (Bài 2 trang 105 SGK Đại Số 10): a ) f ( x ) = ( 3×2 – 10 x + 3 ) ( 4 x – 5 ) – Tam thức 3×2 – x có hai nghiệm x = 0 và x = 1/3, hệ số a = 3 > 0. ⇒ 3×2 – x mang dấu + khi x < 0 hoặc x > 1/3 và mang dấu – khi 0 < x < 1/3 .
– Tam thức 3 – x2 có hai nghiệm x = √ 3 và x = – √ 3, thông số a = – 1 < 0
⇒ 3 – x2 mang dấu – khi x < – √ 3 hoặc x > √ 3 và mang dấu + khi – √ 3 < x < √ 3 .
– Tam thức 4x2 + x – 3 có hai nghiệm x = – 1 và x = 3/4, thông số a = 4 > 0 . * Ví dụ 1 (Bài 3 trang 105 SGK Đại Số 10): Giải các bất phương trình sau a ) 4×2 – x + 1 < 0
b ) - 3x2 + x + 4 ≥ 0
° Lời giải ví dụ 1 (bài 3 trang 105 SGK Đại Số 10): a ) 4×2 – x + 1 < 0
– Xét tam thức f ( x ) = 4x2 – x + 1
– Ta có : Δ = - 15 < 0 ; a = 4 > 0 nên f ( x ) > 0 ∀ x ∈ R * Ví dụ 1 (Bài 4 trang 105 SGK Đại Số 10): Tìm các giá trị của tham số m để các phương trình sau vô nghiệm a ) ( m – 2 ) x2 + 2 ( 2 m – 3 ) x + 5 m – 6 = 0 ° Lời giải ví dụ 1 (bài 4 trang 105 SGK Đại Số 10): a ) ( m – 2 ) x2 + 2 ( 2 m – 3 ) x + 5 m – 6 = 0 ( * ) Bài 53 (trang 145 sgk Đại Số 10 nâng cao): Giải các bất phương trình a ) – 5×2 + 4 x + 12 < 0
b ) 16x2 + 40 x + 25 < 0
c ) 3x2 – 4 x + 4 ≥ 0
d ) x2 – x – 6 ≤ 0
Lời giải: Lời giải: a ) Tập nghiệm T = ( – ∞ ; – 6/5 ) ∪ ( 2 ; + ∞ ) Bài 56 (trang 145 sgk Đại Số 10 nâng cao): Giải các bất phương trình : Lời giải: Bài 55 (trang 145 sgk Đại Số 10 nâng cao): Tìm các giá trị của m để mỗi phương trình sau đây có nghiệm. a ) ( m-5 ) x2-4mx+m-2 = 0 Lời giải: a ) Bài 54 (trang 145 sgk Đại Số 10 nâng cao): Giải các bất phương trình sau: Do đó, tập nghiệm của bất phương trình đã cho là: 1. Bài tập về Bất Phương Trình: Bài 1/ BPT bậc nhất 1.1. Giải các bất phương trình sau:
[ Gợi ý cách nhớ dấu của tam thức khi có 2 nghiệm : Trong trái ngoài cùng ]
Cách xét dấu của tam thức bậc 2
– Lập bảng xét dấu dựa vào dấu của thông số a
– Dựa vào bảng xét dấu và Tóm lạiBất phương trình bậc hai một ẩn ax2 + bx + c > 0 (hoặc ≥ 0; < 0; ≤ 0)
Giải bất phương trình bậc 2
Để giải BPT bậc hai ta vận dụng định lí về dấu của tam thức bậc hai .
Dấu của f(x) được cho trong bảng sau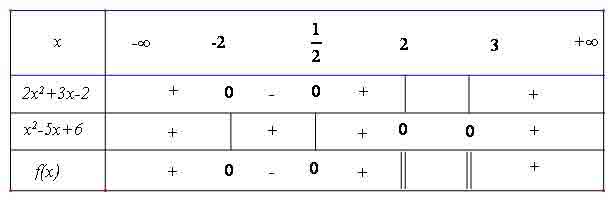
Tập nghiệm của bất phương trình đã cho là

Từ đó suy ra tập nghiệm của hệ là S = ( − 1 ; 1/3 )3. Phương trình – Bất phương trình chứa ẩn trong dấu GTTĐ


4. Phương trình – Bất phương trình chứa ẩn trong dấu căn
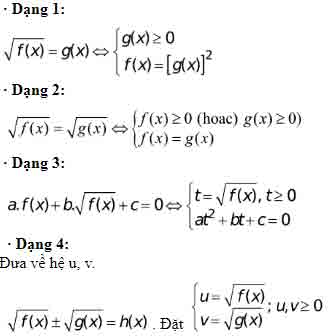

Bất phương trình quy về bậc nhất

Giải và biện luận bpt dạng ax + b < 0
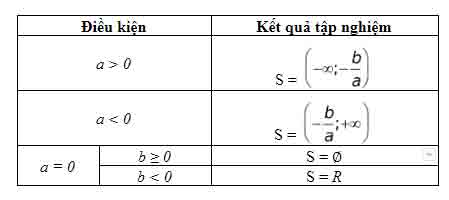
1.1. Hệ bất phương trình bậc nhất một ẩn
1.2. Dấu nhị thức bậc nhất
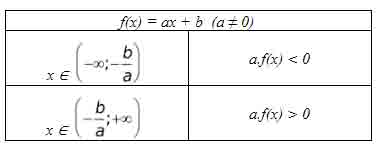
2. Bất phương trình tích
∙ Cách giải : Lập bxd của P ( x ). Q ( x ). Từ đó suy ra tập nghiệm của ( 1 ) .3. Bất phương trình chứa ẩn ở mẫu

Chú ý : Không nên qui đồng và khử mẫu .4. Bất phương trình chứa ẩn trong dấu GTTĐ

Bài tập giải bất phương trình lớp 10
Các bài tập về xét dấu tam thức bậc 2, bất phương trình bậc 2 một ẩn
° Dạng 1: Xét dấu của tam thức bậc 2
b ) – 2×2 + 3 x + 5
c ) x2 + 12 x + 36
d ) ( 2 x – 3 ) ( x + 5 )
– Xét tam thức f ( x ) = 5×2 – 3 x + 1
– Ta có : Δ = b2 – 4 ac = 9 – 20 = – 11 < 0 nên f ( x ) cùng dấu với thông số a .
– Mà a = 5 > 0 ⇒ f ( x ) > 0 với ∀ x ∈ R .
b ) – 2×2 + 3 x + 5
– Xét tam thức f ( x ) = – 2×2 + 3 x + 5
– Ta có : Δ = b2 – 4 ac = 9 + 40 = 49 > 0 .
– Tam thức có hai nghiệm phân biệt x1 = – 1 ; x2 = 5/2, thông số a = – 2 < 0
– Ta có bảng xét dấu :

f ( x ) > 0 khi x ∈ ( – 1 ; 5/2 ) – Từ bảng xét dấu ta có :
f ( x ) = 0 khi x = – 1 ; x = 5/2
f ( x ) < 0 khi x ∈ ( – ∞ ; – 1 ) ∪ ( 5/2 ; + ∞ )
c ) x2 + 12 x + 36
– Xét tam thức f ( x ) = x2 + 12 x + 36
– Ta có : Δ = b2 – 4 ac = 144 – 144 = 0 .
– Tam thức có nghiệm kép x = – 6, thông số a = 1 > 0 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 với ∀ x ≠ – 6
f ( x ) = 0 khi x = – 6
d ) ( 2 x – 3 ) ( x + 5 )
– Xét tam thức f ( x ) = 2×2 + 7 x – 15
– Ta có : Δ = b2 – 4 ac = 49 + 120 = 169 > 0 .
– Tam thức có hai nghiệm phân biệt x1 = 3/2 ; x2 = – 5, thông số a = 2 > 0 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 khi x ∈ ( – ∞ ; – 5 ) ∪ ( 3/2 ; + ∞ )
f ( x ) = 0 khi x = – 5 ; x = 3/2
f ( x ) < 0 khi x ∈ ( – 5 ; 3/2 )
b ) f ( x ) = ( 3×2 – 4 x ) ( 2×2 – x – 1 )
c ) f ( x ) = ( 4×2 – 1 ) ( – 8×2 + x – 3 ) ( 2 x + 9 )
d ) f ( x ) = [ ( 3×2 – x ) ( 3 – x2 ) ] / [ 4×2 + x – 3 ]
– Tam thức 3×2 – 10 x + 3 có hai nghiệm x = 1/3 và x = 3, thông số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3 .
– Nhị thức 4 x – 5 có nghiệm x = 5/4 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 khi x ∈ ( 1/3 ; 5/4 ) ∪ x ∈ ( 3 ; + ∞ )
f ( x ) = 0 khi x ∈ S = { 1/3 ; 5/4 ; 3 }
f ( x ) < 0 khi x ∈ ( – ∞ ; 1/3 ) ∪ ( 5/4 ; 3 )
b ) f ( x ) = ( 3x2 – 4 x ) ( 2x2 – x – 1 )
– Tam thức 3x2 – 4 x có hai nghiệm x = 0 và x = 4/3, thông số a = 3 > 0 .
⇒ 3×2 – 4 x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3 .
+ Tam thức 2x2 – x – 1 có hai nghiệm x = – 50% và x = 1, thông số a = 2 > 0
⇒ 2×2 – x – 1 mang dấu + khi x < – 50% hoặc x > 1 và mang dấu – khi – 50% < x < 1 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 ⇔ x ∈ ( – ∞ ; – 50% ) ∪ ( 0 ; 1 ) ∪ ( 4/3 ; + ∞ )
f ( x ) = 0 ⇔ x ∈ S = { – 50% ; 0 ; 1 ; 4/3 }
f ( x ) < 0 ⇔ x ∈ ( – 50% ; 0 ) ∪ ( 1 ; 4/3 )
c ) f ( x ) = ( 4x2 – 1 ) ( – 8x2 + x – 3 ) ( 2 x + 9 )
– Tam thức 4x2 – 1 có hai nghiệm x = – 50% và x = 50%, thông số a = 4 > 0
⇒ 4×2 – 1 mang dấu + nếu x < – 50% hoặc x > 50% và mang dấu – nếu – 50% < x < 50%
– Tam thức – 8x2 + x – 3 có Δ = – 47 < 0, thông số a = – 8 < 0 nên luôn luôn âm .
– Nhị thức 2 x + 9 có nghiệm x = – 9/2 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 khi x ∈ ( – ∞ ; – 9/2 ) ∪ ( – 50% ; 50% )
f ( x ) = 0 khi x ∈ S = { – 9/2 ; – 50% ; 50% }
f ( x ) < 0 khi x ∈ ( – 9/2 ; – 50% ) ∪ ( 50% ; + ∞ )
d ) f ( x ) = [ ( 3x2 – x ) ( 3 – x2 ) ] / [ 4x2 + x – 3 ]
⇒ 4×2 + x – 3 mang dấu + khi x < – 1 hoặc x > 3/4 và mang dấu – khi – 1 < x < 3/4 .
– Ta có bảng xét dấu :

– Từ bảng xét dấu ta có :
f ( x ) > 0 ⇔ x ∈ ( – √ 3 ; – 1 ) ∪ ( 0 ; 1/3 ) ∪ ( 3/4 ; √ 3 )
f ( x ) = 0 ⇔ x ∈ S = { ± √ 3 ; 0 ; 1/3 }
f ( x ) < 0 ⇔ x ∈ ( – ∞ ; – √ 3 ) ∪ ( – 1 ; 0 ) ∪ ( 1/3 ; 3/4 ) ∪ ( √ 3 ; + ∞ )
f ( x ) không xác lập khi x = - 1 và x = 3/4 .
Dạng 2: Giải các bất phương trình bậc 2 một ẩn

d ) x2 – x – 6 ≤ 0
⇒ Bất phương trình đã cho vô nghiệm .
b ) – 3×2 + x + 4 ≥ 0
– Xét tam thức f ( x ) = – 3×2 + x + 4
– Ta có : Δ = 1 + 48 = 49 > 0 có hai nghiệm x = – 1 và x = 4/3, thông số a = – 3 < 0 .
⇒ f ( x ) ≥ 0 khi - 1 ≤ x ≤ 4/3. ( Trong trái dấu a, ngoài cùng dấu với a )
⇒ Tập nghiệm của bất phương trình là : S = [ - 1 ; 4/3 ]

– Điều kiện xác lập : x2 – 4 ≠ 0 và 3×2 + x – 4 ≠ 0
⇔ x ≠ ± 2 và x ≠ 1 ; x ≠ 4/3 .
– Chuyển vế và quy đồng mẫu chung ta được :
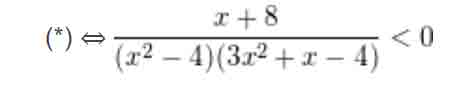
– Nhị thức x + 8 có nghiệm x = – 8
– Tam thức x2 – 4 có hai nghiệm x = 2 và x = – 2, thông số a = 1 > 0
⇒ x2 – 4 mang dấu + khi x < - 2 hoặc x > 2 và mang dấu – khi – 2 < x < 2 .
– Tam thức 3x2 + x – 4 có hai nghiệm x = 1 và x = - 4/3, thông số a = 3 > 0 .
⇒ 3×2 + x – 4 mang dấu + khi x < - 4/3 hoặc x > 1 mang dấu – khi – 4/3 < x < 1 .
– Ta có bảng xét dấu như sau :
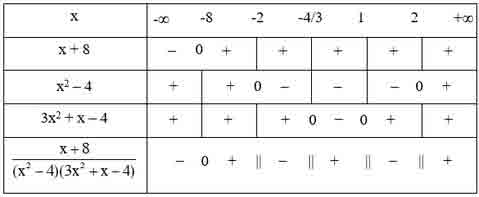
– Từ bảng xét dấu ta có :
( * ) < 0 ⇔ x ∈ ( – ∞ ; – 8 ) ∪ ( - 2 ; - 4/3 ) ∪ ( 1 ; 2 )
d ) x2 – x – 6 ≤ 0
– Xét tam thức f ( x ) = x2 – x – 6 có hai nghiệm x = - 2 và x = 3, thông số a = 1 > 0
⇒ f ( x ) ≤ 0 khi – 2 ≤ x ≤ 3 .
⇒ Tập nghiệm của bất phương trình là : S = [ – 2 ; 3 ] .° Dạng 3: Xác định tham số m thỏa điều kiện phương trình
b ) ( 3 – m ) x2 – 2 ( m + 3 ) x + m + 2 = 0
• Nếu m – 2 = 0 ⇔ m = 2, khi đó phương trình ( * ) trở thành :
2 x + 4 = 0 ⇔ x = – 2 hay phương trình ( * ) có một nghiệm
⇒ m = 2 không phải là giá trị cần tìm .
• Nếu m – 2 ≠ 0 ⇔ m ≠ 2 ta có :
Δ ’ = b ’ 2 – ac = ( 2 m – 3 ) 2 – ( m – 2 ) ( 5 m – 6 )
= 4 mét vuông – 12 m + 9 – 5 mét vuông + 6 m + 10 m – 12
= – mét vuông + 4 m – 3 = ( – m + 3 ) ( m – 1 )
– Ta thấy ( * ) vô nghiệm ⇔ Δ ’ < 0 ⇔ ( - m + 3 ) ( m – 1 ) < 0 ⇔ m ∈ ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ )
– Vậy với m ∈ ( - ∞ ; 1 ) ∪ ( 3 ; + ∞ ) thì phương trình vô nghiệm .
b ) ( 3 – m ) x2 – 2 ( m + 3 ) x + m + 2 = 0 ( * )
• Nếu 3 – m = 0 ⇔ m = 3 khi đó ( * ) trở thành - 6 x + 5 = 0 ⇔ x = 5/6
⇒ m = 3 không phải là giá trị cần tìm .
• Nếu 3 – m ≠ 0 ⇔ m ≠ 3 ta có :
Δ ’ = b ’ – ac = ( m + 3 ) 2 – ( 3 – m ) ( m + 2 )
= mét vuông + 6 m + 9 – 3 m – 6 + mét vuông + 2 m
= 2 mét vuông + 5 m + 3 = ( m + 1 ) ( 2 m + 3 )
– Ta thấy ( * ) vô nghiệm ⇔ Δ ’ < 0 ⇔ ( m + 1 ) ( 2 m + 3 ) < 0 ⇔ m ∈ ( - 3/2 ; - 1 )
– Vậy với m ∈ ( - 3/2 ; - 1 ) thì phương trình vô nghiệm .

b ) Tam thức 16×2 + 40 x + 25 có :
∆ ’ = 202 – 16.25 = 0 và thông số a = 16 > 0
Do đó ; 16×2 + 40 x + 25 ≥ 0 ; ∀ x ∈ R
Suy ra, bất phương trình 16×2 + 40 x + 25 < 0 vô nghiệm
Vậy S = ∅
c ) Tam thức 3x2 – 4 x + 4 có ∆ ’ = ( - 2 ) 2 – 4.3 = - 10 < 0
Hệ số a = 3 > 0
Do đó, 3×2 – 4 x + 4 ≥ 0 ; ∀ x ∈ R
Vậy tập nghiệm của bất phương trình đã cho là S = R .
d ) Tam thức x2 – x – 6 có hai nghiệm là 3 và – 2
Hệ số a = 1 > 0 do đó, x2 – x – 6 khi và chỉ khi – 2 ≤ x ≤ 3
Do đó, tập nghiệm của bất phương trình đã cho là S = [ – 2 ; 3 ] .
b ) Bất phương trình vô nghiệm vì Δ ‘ < 0 và a = 16 > 0
c ) Tập nghiệm là R vì 3×2 – 4 x + 4 có Δ ‘ < 0 và thông số a = 3 > 0
d ) Tập nghiệm T = [ – 2 ; 3 ]





b ) ( m + 1 ) x2 + 2 ( m-1 ) x + 2 m – 3 = 0
+ ) khi m – 5 = 0 ⇒ m = 5 phương trình trở thành :
– 20 x + 3 = 0 ⇒ x = 3/20
+ ) khi m – 5 ≠ 0 ⇒ m ≠ 5, phương trình có nghiệm khi và chỉ khi :
Δ ’ = ( – 2 m ) 2 – ( m – 2 ) ( m – 5 ) ≥ 0
⇒ 4 mét vuông – ( m2-5m-2m+10 ) ≥ 0 ⇒ 4 mét vuông – mét vuông + 7 m – 10 ≥ 0

Do đó, m = – 1 thỏa mãn nhu cầu đầu bài .
+ Trường hợp 2 : Nếu m ≠ – 1, để phương trình đã cho có m nghiệm khi và chỉ khi :


Lập bảng xét dấu :

Do đó, tập nghiệm của bất phương trình đã cho là :
S = ( – ∞ ; 1 ) ∪ ( 7 ; + ∞ )
b ) Ta có :

* Lại có : – x2 + 4 x – 3 = 0 ⇔ x = 1 ; x = 3
Và x2 – 3 x – 10 = 0 ⇔ x = 5 ; x = – 2
+ Ta có bảng xét dấu :

Do đó, tập nghiệm của bất phương trình đã cho là :
S = ( – ∞ ; – 2 ) ∪ [ 1 ; 3 ] ∪ ( 5 ; + ∞ )
c ) Ta có : 2 x + 1 = 0 ⇔ x = – 50%
x2 + x – 30 = 0 ⇔ x = 5 và x = – 6
Ta có bảng xét dấu :

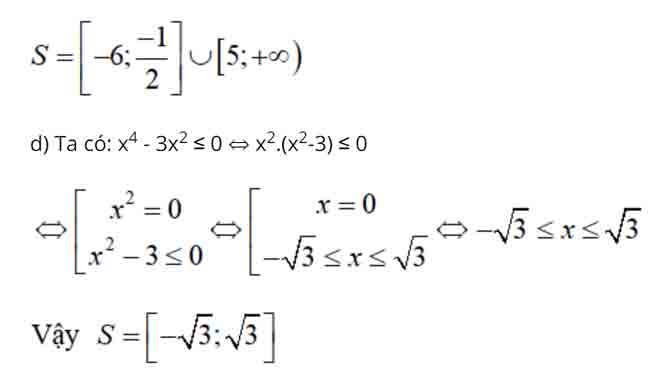












Source: https://camnangbep.com
Category: Học tập
