Công thức cấp số cộng: công thức tính cấp số cộng, công thức tính tổng cấp số cộng, bài tập cấp số cộng có lời giải…
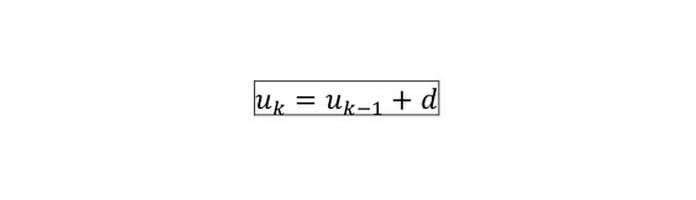
Định nghĩa cấp số cộng
Cấp số cộng ![]() là dãy số xác định bởi:
là dãy số xác định bởi:
![]()
![]() với k=1, 2, .., n – 1
với k=1, 2, .., n – 1
a1 được gọi là số hạng tiên phong, an là số hạng cuối, ak là số hạng thứ k của cấp số cộng ; n được gọi là số số hạng của cấp số cộng ; d được gọi là công sai của cấp số cộng. Sở dĩ có thuật ngữ công sai này là vìa2 – a1 = a3 – a2 = … = an – an-1 = d .Cấp số cộng còn hoàn toàn có thể được đặc trưng bởi đẳng thức ak + 1 – 2 ak + ak-1 = 0 với mọi k = 2, …, n-1. Hay là ak = 50% ( ak-1 + ak + 1 ), số ở giữa bằng trung bình cộng hai số đứng cạnhNgoài những cấp số cộng có hữu hạn thành phần, người ta còn xét những cấp số cộng có vô hạn thành phần. Ví dụ dãy những bội số dương của 3 là một cấp số cộng có vô hạn thành phần với số hạng đầu là 3 và công sai là 3 .
Công thức cấp số cộng
Số hạng tổng quát của cấp số cộng
![Rendered by QuickLaTeX.com \[\begin{array}{l} {u_n} = {u_{n - 1}} + d\\ {u_{n + 1}} = {u_n} + d\\ {u_n} = {u_1} + (n - 1)d \end{array}\]](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-9f0e779b4b0a0334c139630c81be36e9_l3.png)
Trong đó : là số hạng đầu, d là công sai
Tính chất của cấp số cộng
![]()
Với :
![]()
![]()
Tổng của n số hạng đầu của cấp số cộng
![Rendered by QuickLaTeX.com \[\begin{array}{l} {S_n} = {u_1} + {u_2} + ... + {u_n} = \frac{{n({u_1} + {u_n})}}{2}\\ {S_n} = \frac{{n{\rm{[}}2{u_1} + (n - 1)d{\rm{]}}}}{2} \end{array}\]](https://sotayhoctap.com/wp-content/ql-cache/quicklatex.com-3c9a63ea3e79b6b567aeeed79d22d861_l3.png)
Các công thức liên quan đến cấp số cộng
Hai bài toán cơ bản tương quan đến dãy số hoàn toàn có thể giải khá thuận tiện so với cấp số cộng. Cụ thể– Công thức tính số hạng tổng quát của cấp số cộng :ak = a + ( k-1 ) d .– Công thức tính tổng n số hạng tiên phong của cấp số cộng :
![]()
Ở đây khi chứng tỏ công thức thứ nhất, ta đã dùng sáng tạo độc đáo của Gauss ( khi ông còn là 1 cậu bé ) khi ông tính tổng 1 + 2 + … + 99 + 100 rằng 1 + 100 = 2 + 99 = … = 50 + 51 gồm 50 cặp số, mỗi cặp có tổng bằng 101 .Cuối cùng, cũng cần nhắc đến công thức tính số số hạng của một cấp số cộng khi biết số hạng đầu, số hạng cuối và công sai :Số số hạng = [ ( Số hạng đầu – Số hạng cuối ) : công sai ] + 1Đây chính là công thức của bài toán trồng cây quen thuộc ở cấp 2 !
Bài tập cấp số cộng có lời giải
Ví dụ 1: Cho 3 số dương a, b, c. Chứng minh rằng điều kiện cần và đủ để dãy số ![]() lập thành một cấp số cộng có công sai dương là dãy số
lập thành một cấp số cộng có công sai dương là dãy số ![]() là một cấp số cộng.
là một cấp số cộng.
Bài giải :Dãy số là một cấp số cộng
![]()
![]()
Vậy lập thành một cấp số cộng .Ví dụ 2 :
Biết rằng dãy số thực dương ![]() là một cấp số cộng, chứng minh hệ thức :
là một cấp số cộng, chứng minh hệ thức :
![]()
Bài giải :
Ta có ![]()
Tương tự ![]()
Vế trái của ( 1 ) thành :
![]()
![]()
Ví dụ 3 : Cho 2 cấp số cộng
![]() có công sai
có công sai ![]()
và ![]() có công sai
có công sai ![]()
Gọi tổng của n số hạng đầu của mỗi cấp số theo thứ tự là ![]() và
và ![]() . Tìm tỉ số
. Tìm tỉ số ![]()
Bài giải
Ta có ![]() và
và ![]() nên
nên ![]()
![]()
So sánh (1) và (2) => n=21 nên ![]()
Mời những bạn xem thêm video bài giản “ Cấp số cộng ” :
5
/
5 ( 2 bầu chọn )
Source: https://camnangbep.com
Category: Học tập
