Bài tập liên quan đến giá trị tức thời của điện áp và dòng điện là những bài tập khó sử dụng công thức vuông pha và phương pháp đường tròn lượng giác là chủ yếu.
BÀI TẬP LIÊN QUAN ĐẾN GIÁ TRỊ TỨC THỜI CỦA ĐIỆN ÁP VÀ DÒNG ĐIỆN TRONG MẠCH ĐIỆN XOAY CHIỀU VÀ DAO ĐỘNG ĐIỆN TỪ.
A.VẤN ĐỀ:
Trong những đề thi ĐH và CĐ thường cho dạng trắc nghiệm xác lập những giá trị tức thời của điện áp hoặc dòng điện trong mạch điện xoay chiều. Dạng này có nhiều cách giải. Sau đây là 3 cách thường thì. Xét những ví dụ sau :
Ví dụ 1. Xác định điện áp tức thời.
Đặt điện áp xoay chiều có u = 100 \ ( \ sqrt { 2 } \ ) cosωt ( V ) vào hai đầu đoạn mạch gồm điện trở R tiếp nối đuôi nhau với tụ điện C có ZC = R.Tại thời gian điện áp tức thời trên điện trở là 50V và đang tăng thì điện áp tức thời trên tụ là :A. – 50V. B. – 50 \ ( \ sqrt { 3 } \ ) V. C. 50V. D. 50 \ ( \ sqrt { 3 } \ ) V .
Giải cách 1: Dùng phương pháp đại số: R = ZC =>UR = UC.
Ta có : U2 = UR2 + Uc2 = 2UR2 => UR = 50 \ ( \ sqrt { 2 } \ ) V = UC. Mặt khác : \ ( tan \ varphi = \ frac { – Z_ { C } } { R } = – 1 \ rightarrow \ varphi = – \ frac { \ pi } { 4 } \ )Suy ra pha của i là ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ). Xét đoạn chứa R : uR = U0Rcos ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ) = 50 cos ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ) = \ ( \ frac { 1 } { 2 } \ )Vì uR đang tăng nên u’R > 0 suy ra sin ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ) < 0 vậy ta lấy sin ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ) = – \ ( \ frac { \ sqrt { 3 } } { 2 } \ ) ( 1 )và uC = U0C. cos ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) - \ ( \ frac { \ pi } { 2 } \ ) ) = U0C. sin ( \ ( \ omega t + \ frac { \ pi } { 4 } \ ) ) ( 2 )Thế U0C = 100V và thế ( 1 ) vào ( 2 ) ta có uC = – 50 \ ( \ sqrt { 3 } \ ) V .
B.PHƯƠNG PHÁP GIẢI – CÔNG THỨC:
Từ ví dụ trên ta thấy dùng vòng tròn lượng giác hoặc dùng các công thức vuông pha sẽ giải nhanh hơn
I.Dùng giản đồ vectơ hay phương pháp đường tròn lượng giác:
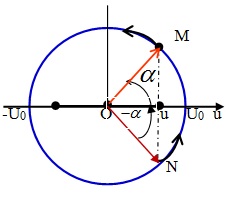
+ Ta xét : \ ( u = U_ { 0 } cos ( \ omega t + \ varphi ) \ ) được trình diễn bằng OM quay quanh vòng tròn tâm O nửa đường kính U0, quay ngược chiều kim đồng hồ đeo tay với vận tốc góc ω ,+ Có 2 điểm M, N hoạt động tròn đều có hình chiếu lên Ou là u, thì :- N có hình chiếu lên Ou lúc u đang tăng ( thì chọn góc âm phía dưới ) ,- M có hình chiếu lên Ou lúc u đang giảm ( thì chọn góc dương phía trên )=> vào thời gian t ta xét điện áp u có giá trị u và đang biến hóa :- Nếu u theo chiều âm ( đang giảm ) ta chọn M rồi tính góc \ ( \ alpha = \ widehat { U_ { 0 } OM } \ )- Nếu u theo chiều dương ( đang tăng ) ta chọn N và tính góc \ ( \ alpha = – \ widehat { U_ { 0 } OM } \ )
Chọn B.
Ví dụ 2. Tìm khoảng thời gian ngắn nhất để điện áp biến thiên từ giá trị u1 đến u2
Đặt vào hai đầu một đoạn mạch RLC một điện áp có PT : \ ( u = 220 \ sqrt { 2 } cos ( 100 \ pi t ) ( V ) \ )Tính thời hạn từ thời gian u = 0 đến khi u = 110 \ ( \ sqrt { 2 } \ ) ( V )
Giảỉ :Với Tần số góc: ω=100π (rad/s)
Cách 1: Chọn lại gốc thời gian: t= 0 lúc u=0 và đang tăng, ta có PT mới : \(u=220\sqrt{2}cos(100\pi t-\frac{\pi }{2})(V)\)và u’ > 0. Khi u =110\(\sqrt{2}\) V lần đầu ta có: cos(100πt )(V)= \(\frac{1}{2}\) và sin(100πt – \(\frac{\pi }{2}\) )(V)
Giải hệ PT ta được t = 1/600 ( s )
II.Các công thức vuông pha, cùng pha:
QUAN HỆ GIỮA CÁC GIÁ TRỊ TỨC THỜI VỚI GIÁ TRỊ HIỆU DỤNG (HAY CỰC ĐẠI)
1. Đoạn xoay chiều chỉ có trở thuần
![]()
+Biểu thức điện áp và dòng điện trong mạch: u(t) = U0cos(ωt +φ)=>
![]()
i, u cùng pha.
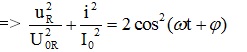
2. Đọan mạch chỉ có tụ điện :
![]()
+Biểu thức điện áp ở hai đầu mạch điện và cường độ dòng điện trong mạch:
Giả sử :u = U0coswωt => i = I0cos ( ωt + π / 2 )Nếu : i = I0cosωt => u = U0cos ( ωt – π / 2 )Nếu : i = I0cos ( ωt + φi ) => u = U0cos ( ωt – π / 2 + φi )
u trễ pha hơn i một góc : \(\frac{\pi }{2}\)
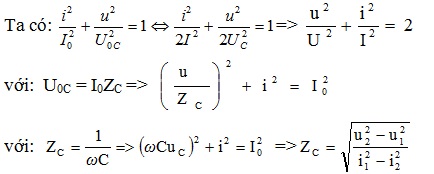
3.Mạch điện xoay chiều chỉ có cuộn cảm :
![]()
+ Biểu thức dòng điện trong mạch :Giả sử i = I0cosωt+ Biểu thức điện áp ở hai đầu mạch điện :uL = U0cos ( ωt + π / 2 )Nếu uL = U0cosωt => i = I0cos ( ωt – π / 2 )Nếu i = I0cos ( ωt + φi ) uL = U0cos ( ωt + π / 2 + φi )
u sớm pha hơn i một góc : \(\frac{\pi }{2}\)
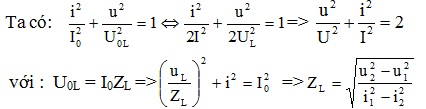
4.Mạch điện xoay chiều chứa L và C: uLC vuông pha với i:
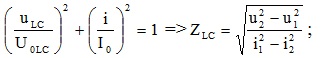
5. Đoạn mạch có R và L : uR vuông pha với uL
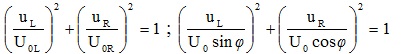
6. Đoạn mạch có R và C: uR vuông pha với uC
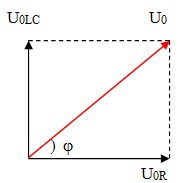
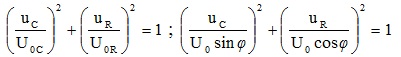
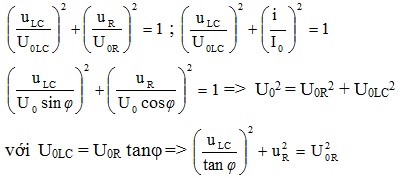
8. Từ điều kiện cộng hưởng ω02LC = 1 :
– Xét với ω đổi khác
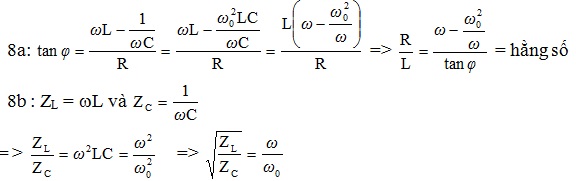
=> đoạn mạch có tính cảm kháng ZL > ZC => ωL > ω0=> đoạn mạch có tính dung kháng ZL < ZC => ωC < ω0=> khi cộng hưởng ZL = ZC => ω = ω0
8c : I1 = I2 < Imax => ω1ω2 = ω02 Nhân thêm hai vế LC
=> ω1. ω2LC = ω02LC = 1=> ZL1 = ω1L và ZC2 = 1 / ω2C=> ZL1 = ZC2 và ZL2 = ZC1
8d : Cosφ1 = cosφ2 => ω1ω2LC = 1 thêm điều kiện L = CR2
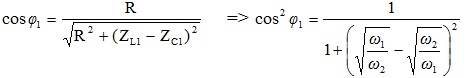
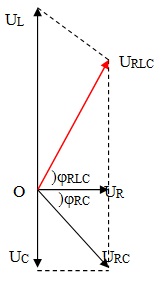
9. Khi L thay đổi ; điện áp hai đầu cuộn cảm thuần L => URC ⊥URLC
=> từ Gỉan đồ Véc tơ:
ULmax <=> tanjRC. tanφRLC = – 1
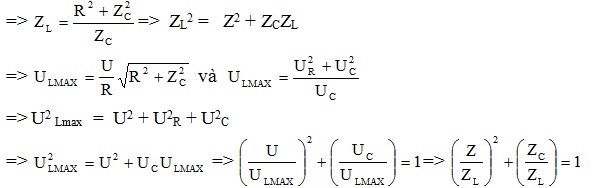
10. Khi C thay đổi ; điện áp hai đầu tụ C => URL^URLC
=> UCmax <=> tanφRL. tanφRLC = – 1
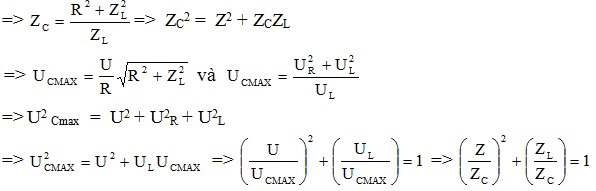
11. Khi URL ⊥ URC
![]()
12. Điện áp cực đại ở hai đầu tụ điện C khi ω thay đổi
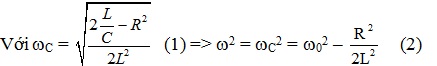
=> cách viết kiểu ( 2 ) mới dễ nhớ hơn ( 1 )với ZL = ωCL và ZC = 1 / ωCC => \ ( \ frac { Z_ { L } } { Z_ { C } } = { \ omega _ { C } } ^ { 2 } LC = \ frac { { \ omega _ { C } } ^ { 2 } } { { \ omega _ { 0 } } ^ { 2 } } \ )
=> từ \(U_{Cmax}=\frac{2LU}{R\sqrt{4LC-R^{2}C^{2}}}\)(3) => từ (2) và (3) suy dạng công thức mới
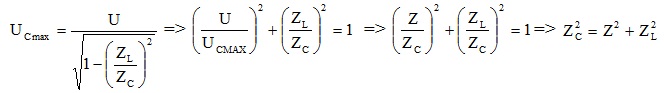
=> 2tanφRL.tanφRLC = – 1 => \((\frac{U}{U_{Cmax}})^{2}+(\frac{{\omega _{C}}^{2}}{{\omega _{0}}^{2}})=1\)
13. Điện áp ở đầu cuộn dây thuần cảm L cực đại khi ω thay đổi
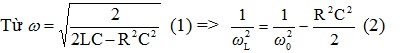
=> cách viết kiểu ( 2 ) mới dễ nhớ hơn ( 1 )=> từ \ ( U_ { Lmax } = \ frac { 2LU } { R \ sqrt { 4LC – R ^ { 2 } C ^ { 2 } } } \ ) ( 3 ) => từ ( 2 ) và ( 3 ) suy dạng công thức mới
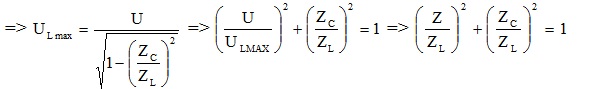
=> \({Z_{L}}^{2}=Z^{2}+{Z_{C}}^{2}\)=> 2tanφRC.tanφRLC = – 1 => \((\frac{U}{U_{Lmax}})^{2}+(\frac{{\omega _{0}}^{2}}{{\omega _{L}}^{2}})=1\)
14. Máy phát điện xoay chiều một pha
Từ thông \ ( \ Phi = \ Phi _ { 0 } cos ( \ omega t + \ varphi ) \ ) ; Suất điện động cảm ứng
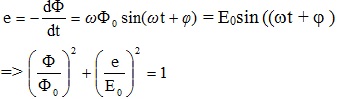
15. Mạch dao động LC lý tưởng:
+ Điện tích trên tụ điện trong mạch xê dịch : q = Q0 cos ( ωt + φ ) .+ Điện áp giữa hai bản tụ điện : u = \ ( \ frac { q } { C } \ ) = U0 cos ( ωt + φ ). Với Uo = \ ( \ frac { q_ { 0 } } { C } \ )
Nhận xét: Điện áp giữa hai bản tụ điện CÙNG PHA với điện tích trên tụ điện
+ Cường độ dòng điện trong cuộn dây :i = q ‘ = – ωq0sin ( ωt + φ ) = I0cos ( ωt + φ + \ ( \ frac { \ pi } { 2 } \ ) ) ; với I0 = q0ω .
Nhận xét : Cường độ dòng điện VUÔNG PHA VỚI Điện tích và điện áp trên 2 bản tụ điện.
+ Hệ thức liên hệ :
![]()
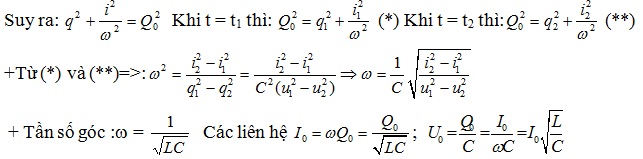
C. VẬN DỤNG:
1. Bài tập:
Bài 1. Đặt điện áp \(u=U_{0}cos\omega t\) vào 2 đầu cuộn cảm thuần có \(L=\frac{1}{3\pi }H\) .ở thời điểm t1 các giá trị tức thời của u và i lần lượt là 100V và -2,5\(\sqrt{3}\)A. ở thời điểm t2 có giá trị là 100\(\sqrt{3}\)V và -2,5A. Tìm ω
Giải: Do mạch chỉ có L nên u và i luôn vuông pha nhau.
Phương trình của i có dạng : \ ( i = I_ { 0 } cos ( \ omega t – \ frac { \ pi } { 2 } ) = I_ { 0 } sin \ omega t \ ) ( 1 )và Phương trình của i có dạng : \ ( u = U_ { 0 } cos \ omega t \ ) ( 2 )Từ ( 1 ) và ( 2 ) suy ra \ ( ( \ frac { i } { I_ { 0 } } ) ^ { 2 } + ( \ frac { u } { U_ { 0 } } ) ^ { 2 } = 1 \ )Ta có hệ :
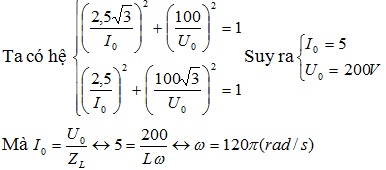
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay
Source: https://camnangbep.com
Category: Học tập
