HỆ BA PHƯƠNG TRÌNH BẬC NHẤT BA ẨN
Phương trình bậc nhất ba ẩn có dạng tổng quát là
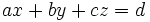 trong đó x, y, z là ba ẩn; a, b, c, d là các hệ số và a, b, c không đồng thời bằng 0.
trong đó x, y, z là ba ẩn; a, b, c, d là các hệ số và a, b, c không đồng thời bằng 0.
trong đó x, y, z là ba ẩn ; a, b, c, d là những thông số và a, b, c không đồng thời bằng 0 .
Hệ ba phương trình bậc nhất ba ẩn có dạng tổng quát là:
Bạn đang đọc: HỆ BA PHƯƠNG TRÌNH BẬC NHẤT BA ẨN
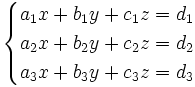 trong đó x, y, z là ẩn; các chữ còn lại là các hệ số.
trong đó x, y, z là ẩn; các chữ còn lại là các hệ số.
trong đó x, y, z là ẩn ; những chữ còn lại là những thông số .
Mỗi bộ ba số (x0;y0;z0) là nghiệm đúng cả ba phương trình của hệ được gọi là một nghiệm của hệ phương trình. Chẳng hạn, 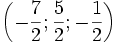
là nghiệm của hệ phương trình
là nghiệm của hệ phương trình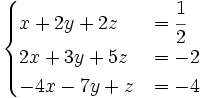 Dạng đặc biệt: Hệ phương trình (2):
Dạng đặc biệt: Hệ phương trình (2):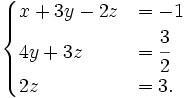
Hệ phương trình ( 2 ) :Hệ này có nghiệm là 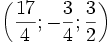 .Hệ phương trình (2) trên có dạng đặc biệt: Phương trình trên cùng có đủ ba ẩn; phương trình thức hai có hai ẩn y và z, khuyết ẩn x; phương trình ba có một ẩn z, khuyết ẩn x và ẩn y. Người ta thường gọi là hệ phương trình dạng tam giác.
.Hệ phương trình (2) trên có dạng đặc biệt: Phương trình trên cùng có đủ ba ẩn; phương trình thức hai có hai ẩn y và z, khuyết ẩn x; phương trình ba có một ẩn z, khuyết ẩn x và ẩn y. Người ta thường gọi là hệ phương trình dạng tam giác.
Hệ phương trình ( 2 ) trên có dạng đặc biệt quan trọng : Phương trình trên cùng có đủ ba ẩn ; phương trình thức hai có hai ẩn y và z, khuyết ẩn x ; phương trình ba có một ẩn z, khuyết ẩn x và ẩn y. Người ta thường gọi là hệ phương trình
Việc giải hệ phương trình dạng tam giác này rất đơn giản. Từ phương trình cuối tính được z rồi thay vào phương trình thứ hai ta tính được y và cuối cùng thay z và y tính được vào phương trình đầu sẽ tính được x.
Chú ý: Mọi hệ ba phương trình bậc nhất ba ẩn đều biến đổi được về dạng tam giác, bằng phương pháp khử dần ẩn số(*).
Dạng 1. Giải hệ phương trình
Ví dụ 1. Giải hệ
Lời giải
Nhân hai vế của phương trình thứ nhất của hệ (6) với -2 rồi cộng vào phương trình thứ hai theo từng vế tương ứng, nhân hai vế của phương trình thứ nhất với 4 rồi cộng vào phương trình thứ ba theo từng vế tương ứng, ta được hệ phương trình (đã khử x ở hai phương trình cuối)
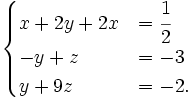 Tiếp tục cộng các vế tương ứng của phương trình thứ hai và phương trình thứ ba của hệ mới nhận được, ta được hệ phương trình tương đương dạng tam giác:
Tiếp tục cộng các vế tương ứng của phương trình thứ hai và phương trình thứ ba của hệ mới nhận được, ta được hệ phương trình tương đương dạng tam giác: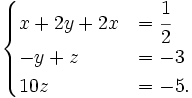 Ta dễ dàng giải ra được
Ta dễ dàng giải ra được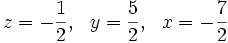
Ta thuận tiện giải ra được
Vậy hệ có một nghiệm là: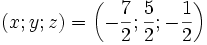
Ví dụ 2:
Hệ phương trình
USD \ left \ { \ begin { align } và x + y + z = 3 \ \ và 2 x – y + 2 z = – 3 \ \ và x-3y-3z = – 5 \ \ \ end { align } \ right. USD
có nghiệm là :
A. (1; 3;–1) B. (1; 3;–2) C. (1; 2; –1) D. (1; –3; –1)
Lời giải
Chọn A.
Giải tự luận:
Cách 1:
Cộng phương trình thứ nhất và thứ hai theo vế, ta được hệ phương trình sau :
USD \ left \ { \ begin { align } và x + y + z = 3 \ \ và 3 x + 3 z = 0 \ \ và x-3y-3z = – 5 \ \ \ end { align } \ right. USD
Nhân hai vế phương trình đầu với 3, xong đem cộngtheo vế với phương trình cuối, ta được hệ
USD \ left \ { \ begin { align } và x + y + z = 3 \ \ và x + z = 0 \ \ và 4 x = 4 \ \ \ end { align } \ right. USD
Từ phương trình cuối ta có USD x = 1, USD thay vào phương trình hai tính được USD z = – 1. USD thay đồng thời vào phương trình đầu thì USD y = 3. USD Vậy nghiệm của hệ là USD ( 1 ; \, 3 ; \, – 1 ). USD
Cách 2:Rút ẩn từ một phương trình thay vào hai phương trình còn lại.
Từ phương trình đầu ta rút được USD z = 3 – x-y, USD đem thay vào hai phương trình còn lại ta được hệ :
\ [ \ left \ { \ begin { align } và z = 3 – x-y \ \ và 2 x – y + 2 z = – 3 \ \ và x-3y-3z = – 5 \ \ \ end { align } \ right. \ ]
Thế phương trình nguồn vào hai phương trình sau ta có hệ :
\ [ \ left \ { \ begin { align } và z = 3 – x-y \ \ và – 3 y = – 9 \ \ và 4 x = 4 \ \ \ end { align } \ right. \ ]
Từ hai phương trình cuối dễ tính được USD x = 1, \, y = 3. USD Thay vào phương trình đầu được USD z = – 1. USD
Vậy nghiệm của hệ là USD ( 1 ; \, 3 ; \, – 1 ). USD
Giải trắc nghiệm:
Bấm máy tính Chọn A .
Dạng 2 : Tìm điềm kiện của tham số để hệ ba phương trình bậc nhất 3 ẩn có nghiệm thỏa điều kiện cho trước ?
Phương pháp giải:
Hệ có dạng: \[\left\{ \begin{align}& {{a}_{1}}x+{{b}_{1}}y+{{c}_{1}}z={{d}_{1}} \\ & {{a}_{2}}x+{{b}_{2}}y+{{c}_{2}}z={{d}_{2}} \\ & {{a}_{3}}x+{{b}_{3}}y+{{c}_{3}}z={{d}_{3}} \\\end{align} \right.\cdot \] Một nghiệm của hệ là bộ 3 số $({{x}_{o}};{{y}_{o}};{{z}_{o}})$ thỏa cả 3 phương trình của hệ. Nguyên tắc chung để giải các hệ phương trình nhiều ẩn là khử bớt ẩn để đưa về các phương trình hay hệ phương trình có số ẩn ít hơn. Để khử bớt ẩn, ta cũng có thể dùng các phương pháp cộng đại số, phương pháp thế như đối với hệ phương trình bậc nhất hai ẩn.
- VÍ DỤ MINH HỌA
Ví dụ 1: Tìm tất cả các giá trị thực của tham số $m$ để hệ:
$\left\{ {\begin{array}{*{20}{c}}
{x + y + \left( {m + 1} \right)z = 2}&{(1)}\\
\begin{array}{l}
3x + 4y + 2z = m + 1\\
2x + 3y – z = 1
\end{array}&\begin{array}{l}
(2)\\
(3)
\end{array}
\end{array}} \right.$
vô số nghiệm ?
A.$m=2$. B.$m=-3$ C.$m=1$ D.$m\ne 2$
Chọn A.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ USD ( 3 ) USD suy ra USD z = 2 x + 3 y – 1 USD. Thế vào hai PT ( 1 ) và ( 2 ) ta được
$\left\{ \begin{array}{l}
x + y + (m + 1)(2x + 3y – 1) = 2\\
3x + 4y + 2(2x + 3y – 1) = m + 1
\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}
(2m + 3)x + (3m + 4)y = m + 3\\
7x + 10y = m + 3
\end{array} \right.$
Ta có :
\ [ D = \ left | \ begin { matrix } 2 m + 3 và 3 m + 4 \ \ 7 và 10 \ \ \ end { matrix } \ right | = 2 – m \ ]
\ [ { { D } _ { x } } = \ left | \ begin { matrix } m + 3 và 3 m + 4 \ \ m + 3 và 10 \ \ \ end { matrix } \ right | = 3 ( m + 3 ) ( 2 – m ) \ ]
\ [ { { D } _ { y } } = \ left | \ begin { matrix } 2 m + 3 và m + 3 \ \ 7 và m + 3 \ \ \ end { matrix } \ right | = – 2 ( m + 3 ) ( 2 – m ) \ ] .
Hệ phương trình có vô số nghiệm USD \ Leftrightarrow D = { { D } _ { x } } = { { D } _ { y } } = 0 \ Leftrightarrow m = 2 USD
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt các giá trị của $m$ ở 3 đáp án A, B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án A.
Ví dụ 2: Tìm tất cả các giá trị thực của tham số $m$ để hệ:
$\left\{ {\begin{array}{*{20}{c}}
{x + y – z = 1}&{(1)}\\
\begin{array}{l}
2x + 3y + mz = 3\\
x + my + 3z = 2
\end{array}&\begin{array}{l}
(2)\\
(3)
\end{array}
\end{array}} \right.$
vô nghiệm ?
A.$m=2$. B.$m=-3$
C.$m=1$ D.$m\ne 2,m\ne -3$
Chọn B.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ ( 1 ) suy ra z = x + y-1. Thay vào ( 2 ) và ( 3 ) ta được
$\left\{ \begin{array}{l}
2x + 3y + m(x + y – 1) = 3\\
x + my + 3(x + y – 1) = 2
\end{array} \right.$
$ \Leftrightarrow \left\{ \begin{array}{l}
(m + 2)x + (m + 3)y = m + 3\\
4x + (m + 3)y = 5
\end{array} \right.$
Ta có :
$D = \left| {\begin{array}{*{20}{c}}
{m + 2}&{m + 3}\\
4&{m + 3}
\end{array}} \right| = (m + 3)(m – 2)$
${D_x} = \left| {\begin{array}{*{20}{c}}
{m + 3}&{m + 3}\\
5&{m + 3}
\end{array}} \right| = (m + 3)(m – 2)$
${D_y} = \left| {\begin{array}{*{20}{c}}
{m + 2}&{m + 3}\\
4&5
\end{array}} \right| = m – 2$
Với: ${\rm{D = }}0 \Leftrightarrow \left[ \begin{array}{l}
m = 2\\
m = – 3
\end{array} \right.$
+ Khi USD m = 2 USD ta có USD \ text { D } = { { D } _ { x } } = { { D } _ { y } } = 0 USD nên hệ phương trình có nghiệm là nghiệm của phương trình USD 4 x + 5 y = 5 \ Leftrightarrow y = \ frac { – 4 } { 5 } x + 1 USD .
Do đó hệ phương trình có nghiệm là USD \ left ( x ; y \ right ) = \ left ( 5 t ; – 4 t + 1 \ right ), \, \, t \ in \ mathbb { R } USD .
+ Khi USD m = – 3 USD ta có USD D = 0, \, { { D } _ { y } } \ ne 0 USD nên hệ phương trình vô nghiệm
Chọn đáp án B .
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt các giá trị của $m$ ở 3 đáp án A, B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án B.
Ví dụ 3: Tìm tất cả các giá trị thực của tham số $m$ để hệ:
$\left\{ \begin{array}{l}
mx + y = 1\\
my + z = 1\\
x + mz = 1
\end{array} \right.$
có nghiệm duy nhất ?
A.$m\ne 1$. B.$m=1$
C.$m=-1$ D.$m\ne -1$
Chọn D.
Lời giải
Cách 1:Giải bằng phương pháp tự luận
Từ ( 2 ) suy ra z = 1 – my. Thay vào ( 3 ) ta được :
$\left\{ \begin{array}{l}
mx + y = 1\\
x – {m^2}y = 1 – m
\end{array} \right.$
Hệ có nghiệm duy nhất khi :
USD \ frac { m } { 1 } \ ne \ frac { 1 } { { – { m ^ 2 } } } \ Leftrightarrow m \ ne – 1 USD
Chọn đáp án D .
Cách 2:Giải bằng phương pháp trắc nghiệm: Lấy lần lượt các giá trị của $m$ ở 3 đáp án B, C thay vào hệ và sử dụng MTCT để giải. Chọn đáp án B.
-
2. BÀI TẬP
1. Giải các hệ phương trình
a) 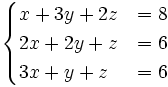
b) 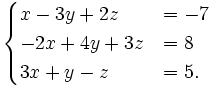
2. Một cửa hàng bán áo sơ mi, quần âu nam và váy nữ. Ngày thứ nhất bán được 12 áo, 21 quần và 18 váy, doanh thu là 5 349 000 đồng. Ngày thứ hai bán được 16 áo, 24 quần và 12 váy, doanh thu là 5 600 000 đồng. Ngày thứ ba bán được 24 áo, 15 quần và 12 váy, doanh thu là 5 259 000 đồng. Hỏi giá bán mỗi áo, mỗi quần và mỗi váy là bao nhiêu?
3. Giải các hệ phương trình sau bằng máy tính bỏ túi (làm tròn kết quả đến chữ số thập phân thứ hai)
a) 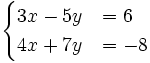
b) 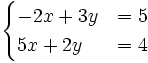
c) 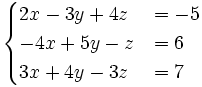
d) 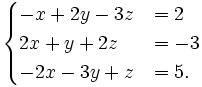
Source: https://camnangbep.com
Category: Học tập
